[cvp07] Subdifferential Optimization Condition

Dec.30, 2019

最后一周的凸分析课程，这次课也最终总结了凸分析研究优化问题的基本思想。本此的概要：

• 切锥和法锥的概念，这两个基本概念对最优点所处条件作了方向性的描述。是基本工具。
• 次梯度和次微分引入使得我们可以研究不可微凸函数的最优性条件。
• 研究在不同类型集合上不同类型函数的最优性条件，使用次梯度和切锥、法锥为工具；

可以看出凸分析使用集合的角度研究优化贯穿始终，例如上周使用MCMC几何框架推出了优化常用的对偶理论。那么本周所得出的最优性条件也可以推导出大家非常熟悉的KKT条件。在本次内容之前我有必要回顾一下之前的章节，以数理整体脉络(其实是要考试了…)：

• 01-凸集、凸包、仿射集、仿射包、锥、生成锥、相对内部

这些基本的集合类型的用处是为了后续描述一些几何上的特性时更加方便。从凸集到仿射包的定义过程是逐渐放宽条件的。他们各自的性质也用到了后续的证明中；相对内部的定义是为了凸函数的研究中，定义域集和通常在整个函数空间的子空间中，此时定义域上内部的概念就失效了，为了更方便研究定义了相对内部的概念。

• 02-凸函数、拟凸函数、共轭函数

函数的上图的凸性和闭性与函数自身的连续性、凸性相联系。凸函数不一定都是连续可微的，而上图是一定存在可描述的。共轭函数的概念非常重要，他描述了函数上图另一种定义方式，即是一组与共轭函数相关的超平面的交集，这是对偶理论的基础。

• 03-回收锥、回收函数

回收方向是函数不增的方向。同样函数的增减性不用导数和微分描述，使用函数上图和定义域的回收方向描述，并且描述最优解的存在性条件。

• 04-超平面

这讲内容与其他部分是分离的。四种分离超平面描述了集合分离的基本类型。而凸分析基于一个基础理论就是所有的凸集都可以写成闭半空间交集的形式；

• 05-凸多面体、极锥

正如线性规划是很多与优化理论教程的开端，凸分析中使用凸多面体集合和顶点的概念分析线性规划问题的最优性条件；而极锥的概念由顶点而来，他描述了与一个集合方向始终成钝角的集合，极锥也是凸分析的重要工具；

• 06-MCMC对偶理论

由极大极小与极小极大的对偶问题出发，使用两类几何问题对应描述，从而得出对偶间隙、弱对偶定理。

• 07-次梯度、最优性条件

使用次梯度分析一般函数的最优点满足的条件。

可见凸分析虽然不讲具体方法，但与凸优化切入的方式思想是相同的，对偶理论后寻找强对偶的条件，也就是最优点条件。

切锥、法锥

可行方向集

definition: 设$C$ 是 $\mathbb{R^n}$ 的子集，$x\in C $ 是向量，$y \in \mathbb{R}^n$ 的向量。 若存在$\bar{\alpha} \gt 0$ 使得 $x + \alpha y \in C ,\ \forall \alpha \in [0, \bar{\alpha}]$ 成立，则称$xy$ 为集合$C$在$x$ 处的可行方向集合。记做$F_C(x)$

$F_C(x)$ 为包含原点的锥；

若$C$是凸集， $\alpha \gt 0$ 以及 $\bar{x} \in C$ 则 $\alpha (\bar{x} -x) \in F_C(x)$

切方向，切锥

definition: $x$ 是$C$中向量， $y$ 是$\mathbb{R^n}$ 中向量， 若存在序列${x_k } \subseteq C$ ，对所有$k$ （对所有路径） 满足$x_k \neq x$ 且 $x_k \rightarrow x,\ \frac{x_k -x}{ ||x_k - x||} \rightarrow \frac{y}{||y||}$ 则称$y$ 是$C$ 在$x$ 处的切方向；这些方向的集合成为$C$在$x$ 处的切锥 (Tangent Cone)， 记做$T_C(x)$ .

从直观上理解，就是一条到达$x$ 的路径序列最后的方向的极限。下面从几何上解释下：

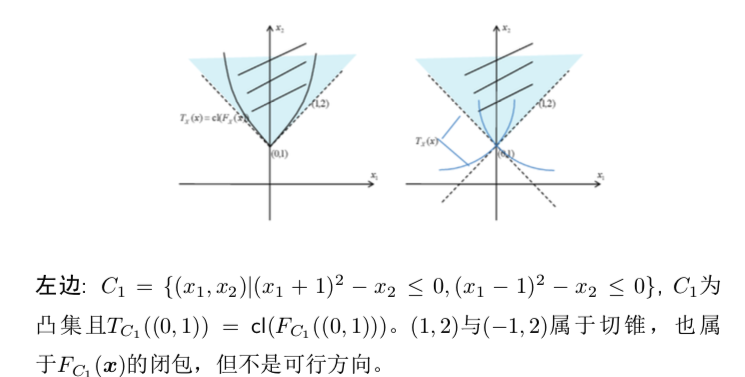
左图中从内部的路径都会有任意的方向，而从边界逼近的路径最后的极限方向是切线。

切锥与可行方向集有如下的性质：

1. $T_C(x)$ 是闭锥；
2. $cl(F_C(x)) \subseteq T_C(x)$
3. 若$C$ 为凸集，则 $F_C(x) , T_C(x)$ 都是凸集；且$cl(F_C(x)) = T_C(x)$

法锥与正则

法锥的定义就更抽象了：

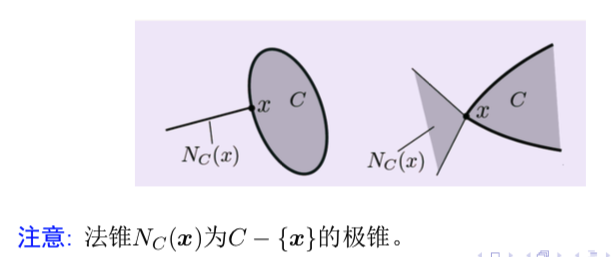
$x$ 是$C$中的向量， 对$\mathbb{R^n}$中的向量$z$ , 若存在序列${ x_k } \subseteq C$, 及${z_k}$ 有 $x_k \rightarrow x,\ z_k \rightarrow z; \ z_k \in T_C(x_k)^{\star}$ 这样的$z$ 成为法向量， 集体成为$C$在$x$处的法锥（normal cone），记做 $N_C(x)$

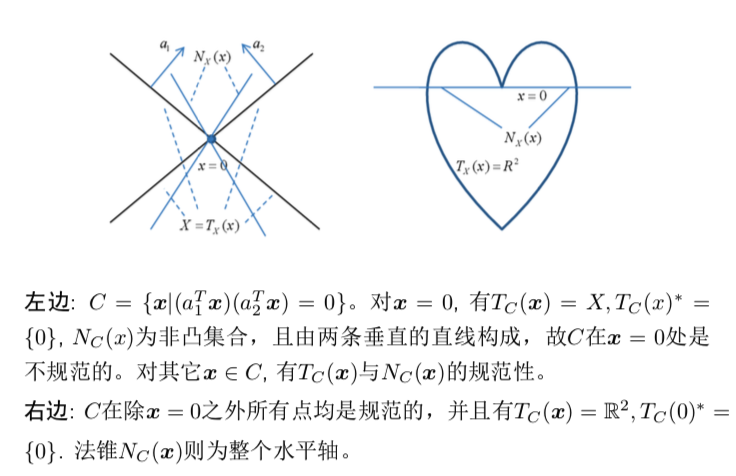
在逼近$x$的路径上，有一个序列总在他切锥的极锥中, 那这个序列最终收敛的方向及时他的法方向；

若有 $N_C(x) = T_C(x)^{\star}$ 则称$C$ 在$x$ 处是正则的或规范的；下面是一个几何例子：

次梯度与次微分

在凸函数不可微的情况下，可用次梯度替代梯度，类似的也可以建立相应的最优性条件；

definition： 次梯度

令$f: \mathbb{R^n} \rightarrow (-\infty, \infty] $ 为正常凸函数， 且$x \in domf$ 若向量$g$ 满足： $f(z) \ge f(x) + g^T(z-x),\ \forall z \in \mathbb{R^n}$ 则称$g$是$f$在$x$ 处的次梯度；

可以看处上述定义就是可微凸函数的一阶条件。从几何上看，$h(z) = f(x) + g^T(z-x)$ 就是在$x$处的一个支撑超平面，函数的上图$epi(f)$ 被包含在他的闭半空间中；

Theorem 次梯度唯一性

若$f$在点$x$处可微， 则$\nabla f(x)$ 是$x$处唯一的次梯度；

definition： 次微分

函数$f$在$x$处的次梯度的全体成为$f$在$x$处的次微分； $\partial f = \{g\in \mathbb{R^n} |\ f(z) \ge f(x) + g^T(x-z),\ \forall z \in \mathbb{R^n} \}$ 若$\partial f$不是空集，则称$f$ 在$x$处是可微分的。

我们约定：

对所有不在定义域的$x$, 其次微分$\partial f(x)$ 为空集；

次微分是一系列闭半空间的交集，所以是闭凸集；

次梯度仅针对正常函数有定义，非正常函数无次梯度；

example:

凸函数最优性充要条件

Theorem:

若$f(x) : C \rightarrow \mathbb{R}$ 为凸函数，且对$\forall x \in \mathbb{R^n}$ , 有$\partial f(x)$ 非空，则$\bar{x}$ 为局部极小点的充分必要条件是： $\bold{0} \in \partial f(\bold{\bar{x}})$

示性函数次微分

$$\delta_C(x) =\left\{ \begin{aligned} 0 && if \ x \in C \\ \infty && otherwise \\ \end{aligned} \right.$$

对示性函数求次微分：

当$x \notin C$ 时，$\partial \delta_C(x) = \empty$， 若$x \in C$ ,$g$ 为示性函数的次梯度，可以求出： $\partial \delta_C(x) = \{g | g^T(z-x) \le 0,\ \forall z \in C \}$ 可以看出示性函数的次微分就是$C$ 在$x$ 处的法锥 $N_C(x)$

最优性条件

凸函数$f$ 在$R^n$ 上取得最小解的充要条件是$0 \in \partial f(x^{\star}) $, 现在来把该最优性条件推广到一般有约束的优化问题；

Theorem: 一般最优性条件：

$X$ 为$\mathbb{R^n}$ 的非空凸子集， 若$ri(dom(f)) \cap ri(X) \neq \empty$, 则$x^\star$ 为$f$ 在$X$ 上的极小点当且仅当： $\exists \ \bold{g} \in \partial f(x^\star)， \bold{g}^T(x-x^\star) \ge 0,\ \forall x \in X$ 成立，即$\bold{-g} \in N_X(x^\star)$

这个一般性结论也不难证明：

proof:

该优化问题等价于: $minimize \ f(x) + \delta_X(x), \\ s.t. \ x \in R^n$ $x^\star$ 是该问题最优解当且仅当： $0 \in \partial (f+\delta_X)(x^\star) = \partial f(x^\star) + \partial \delta_X(x^\star) \\ = \partial f(x^\star) + N_X(x^\star)$ 既有 $-g \in N_X(x^\star)$

Reference

• 老师的课件
• 《Convex Theory 3rd》