[cvp04] Hyperplane

06 Dec 2019 by BY Zhi-kai Yang

Dec. 05 创新岗 XJTU

第四周，在Boyd凸优化教材第一章的练习题中做了大量关于“ 任何闭凸集都可以用超平面刻画：一个凸集是所有包含他的半平面的交集” 的证明；如果对凸函数的上镜图使用此结论，就可以得到其共轭函数的描述，他是下周对偶理论的基础。

PS：这门课可以改名字叫《凸分析》了，优化的内容（方法）只有一次课讲，Stephen Boyd的课程更侧重方法。

超平面

$H = \{x\ |\ a^Tx =b\}$

表示一个$R^n$中$(n-1)$维的超平面，令$\bar{x}$是其中的向量，则超平面可以被等价地定义为：

$H = \{x\ |\ a^Tx=a^T\bar{x}\}$

或者

$H= \bar{x} + \{x |a^Tx=0 \}$

可以看到超平面是与一个子空间平行的仿射集合，向量$a$与该子空间正交，即其法向量；超平面的两侧既是正半空间和负半空间。可能是开的或闭的；

分离超平面

有几种相似的说法，比如超平面$H$分离了$C_1$和$C_2$ 、 $H$是两个集合的分离超平面，两个集合可被分离等，都是指下列的条件：

$a^Tx_1 \le a^Tx_2,\\ x_1\in C_1, x_2 \in C_2$

或

$\sup_{x \in C_1} a^Tx \le \inf_{x \in C_2}a^Tx$

如果将其中一个集合退化成一个单点集${\bar{x}}$ , 那这个超平面就是另一个集合在点$\bar{x}$ 的支撑超平面 （从集合上讲就是切点和切线的关系）

$a^T\bar{x} = \inf_{x\in C}a^Tx$

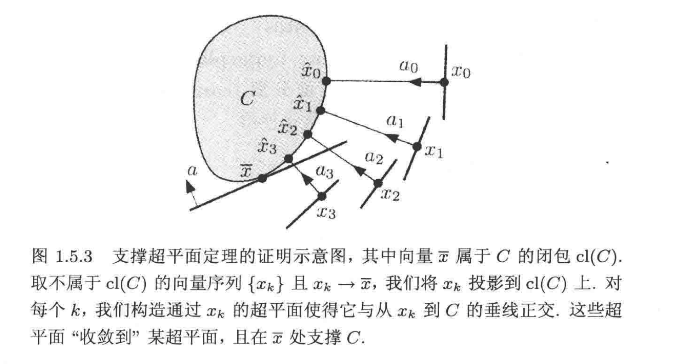
定理1 （支撑超平面定理）

$C$是非空凸集，如果$\bar{x}$不是他的内点，则一定存在通过$\bar{x}$的超平面使得$C$在其闭半空间中。即存在$a^T \neq 0$ , 使得

$a^T\bar{x} \le a^Tx, \ \forall x \in C$

证明使用到了投影定理：

一个点对一个集合做投影就是找到集合中的$z$ 使得$||z-x||^2$最小；同时满足下面的条件 $(z-x^*)^T(x^*-x) \ge 0\\ \forall x \in C$

定理2 分离超平面定理

$C_1$、$C_2$都是非空凸集，如果两者不相交，则一定存在其分离超平面；

Proof: $C = C_1 - C_2 = \{x|x= x_1 - x_2,\ x_1 \in C_1, x_2 \in C_2\}$ $C_1,C_2$不想交意味着原点不属于$C$

则根据支撑超平面定理，点0出存在$C$的支撑超平面： $0 \le a^Tx,\ x \in C$ 得出 $a^Tx_1 \le a^Tx_2$

严格分离

把上文中的等号去掉，严格小于即为严格分离；

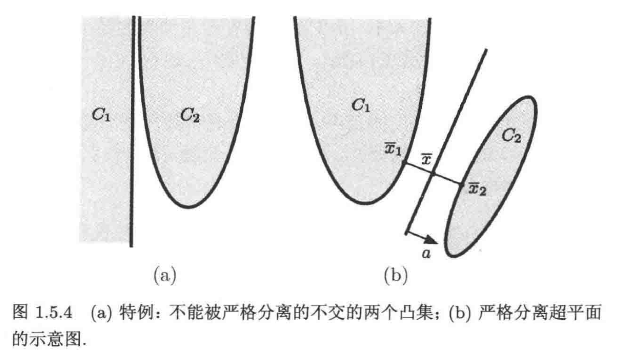
定理3 严格分离定理

对于两个不相交法凸集，两者能被严格分离的等价条件如下：

$C_2-C_1$是闭集
$C_1$是闭的，$C_2$是紧的；
$C_1、C_2$都是多面体；

定理4

集合$C$的凸包是包含$C$的所有的闭半空间的交集；特别的，一个闭凸集的是包含他所有的闭半空间的交集；

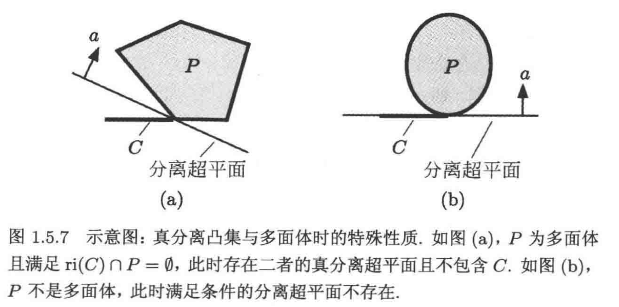
真（正常）分离 Proper Separation

第三类的分离比分离稍强一些，表示能不仅能分离$C1$与$C_2$，且不同时包含 $C_1$与$C_2$; 既满足：

$\sup_{x\in C_1}a^Tx \le \inf_{x\in C_2} a^Tx \\ \inf_{x\in C_1}a^Tx \lt \sup_{x\in C_2} a^Tx$

因为超平面的维度都比集合要低，因此只要其中一个集合不是空集，那么就能找到真分离的超平面；

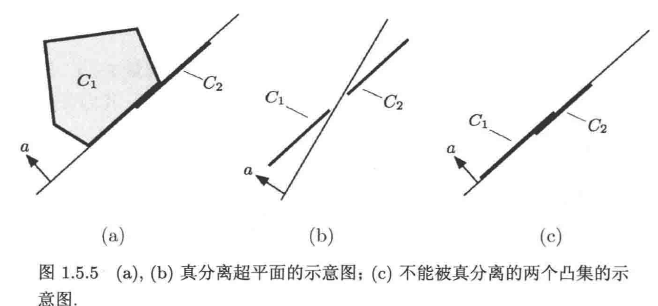
定理5 真分离定理

令$\bar{x}$是空间中的一个向量，则

存在$C$与$\bar{x}$ 的真分离超平面 $\iff$ $\bar{x} \notin ri(C)$

仔细对比下定理1中关于存在支撑超平面的条件，可以发现一个要求是不在内部、真分离要求不在相对内部，可以看出真分离的要求更强一些：

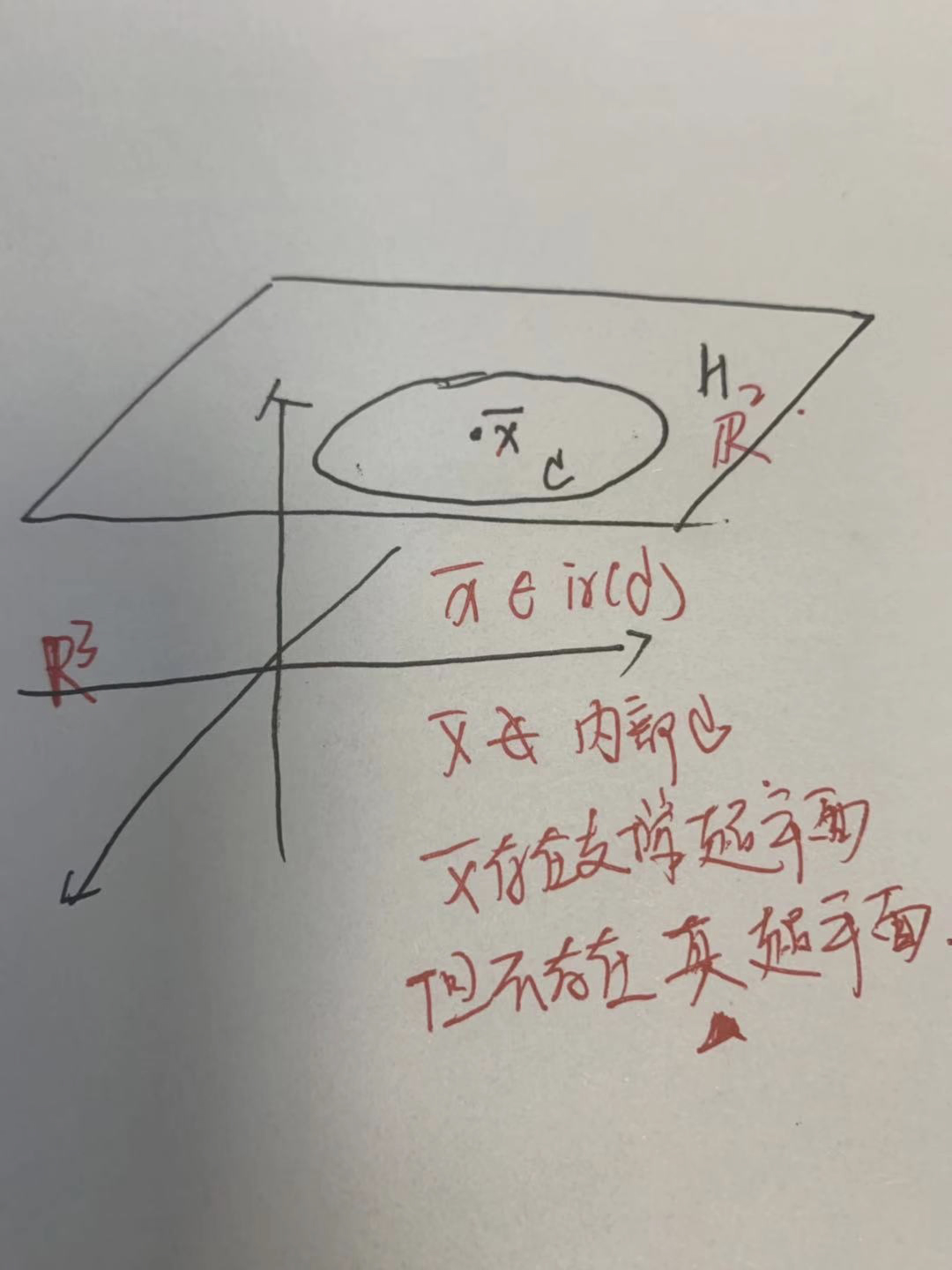
上图中H不是真分离平面，因为他同时包含了点和集合；

两个凸集真分离定理

两个几个存在真分离超平面 $\iff$ $ri(C_1) \cap ri(C_2) = \empty$

当然多面体比较特殊，如果其中一个凸集是多面体也可以保证真分离：

垂直超平面

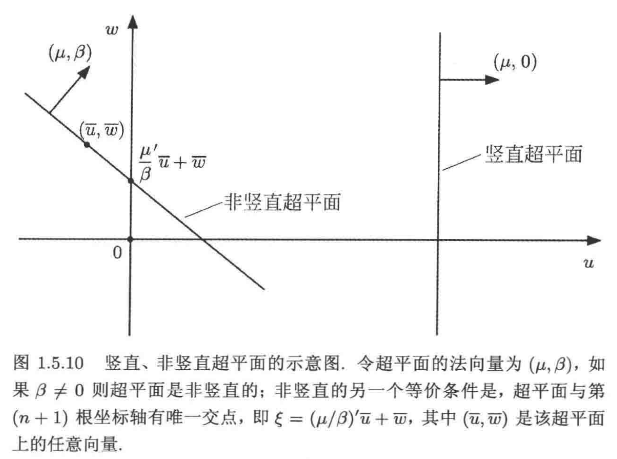
引入垂直超平面的动机是研究函数的上镜图，可以看到函数的上图应该不包含任何垂直的超平面；这一点有更严格的数学定理；

共轭函数的

共轭函数在第二周定义过了，这里使用超平面研究其二次共轭，并引出共轭定理

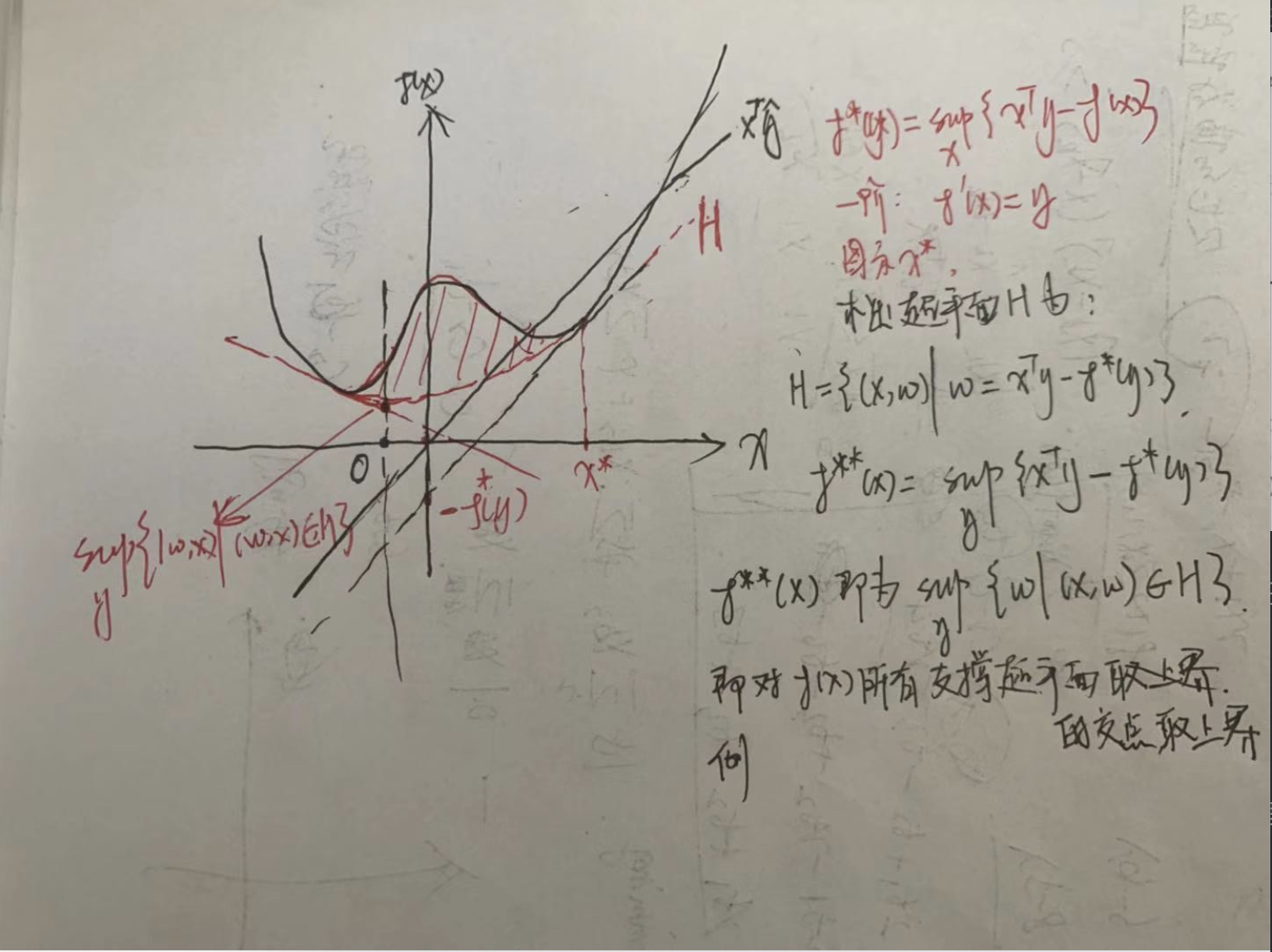
定理7 共轭定理：

（a）恒有：

$f^{**} (x) \le f(x)$

(b) 如果$f$ 是凸函数，则如果$f,f^*,f^{**}$中任意一个是真函数（正常函数），则其余都是正常函数；（正常函数就是不恒取无穷的函数）

(d) 也可以从图中看出来的：函数$f$的闭凸包函数是其二次共轭（二次共轭函数的上图是原函数的闭凸包）好绕口啊！

Reference

《Convex Optimization Theory》
老师的课件

Zhi-Kai Yang