[cvp05] Polyhedron Covexity

• 2019-12-12 创新岗，第五周

• 多面体凸性；包含极点、极锥 与 多面体最优性关系

本周内容概要：

从凸集的顶点入手，分析一般的椎体之间的对偶关系，扩展到多面体锥和多面体集。这些理论可以用来解释线性规划的最优性；

顶点

给定非空凸集$C$, 如果找不到这样的$y\in C, z \in C$, 使得 $x = \alpha y + (1-\alpha)z ,\alpha \in (0,1)$，则这样的点$x$便是集合$C$的一个顶点或称极点（extreme point）；

从集合上想象，以顶点为中心的线段，其两端不可能同时存在于集合；

极点会有一些相关的结论：

• 极点不能由凸集中其他点的凸组合来表示；
• 开集中无极点；
• 凸锥 至多有一个极点，就是原点；
• 凸多面体极点个数是有限的，亦可能没有；
• 多面体上的凹函数至少会在某个极点出取到最小值；

命题1

$C$ 属于超平面$H$的一个半空间中，若$x$ 是集合$C \cap H$ 的顶点，则 $x$ 也是$C $的顶点

proof

若$\bar{x} \in C\cap H$ 且是他的顶点, 反证法，假设$\bar{x}$不是$C$的顶点，则存在$y,z \in C$使得 $\bar{x} = \alpha y + (1-\alpha)z$ 因为$\bar{x} \in H$ 则超平面的等价表示为: $H: {x |a^Tx=a^T\bar{x}}$

因为$C$ 在超平面的闭半空间中，则$y,z$满足：

$a^T \bar{x} \le a^Ty,\ a^T\bar{x} \le a^Tz$

而$\bar{x}$又是$y,z$的凸组合，则 $y, z\in C\cap H$, 进一步 $y, z \in H$ 这与$\bar{x}$ 是$C\cap H$的顶点这一前提相矛盾。

所以，$x$ 一定同时是$C$的顶点；

命题2 极点存在定理

非空闭凸集存在至少一个顶点 $\iff$ 他不包含任何直线，即具有

$${x+\alpha d |\alpha \in R, d \neq 0 }$$

形式的集合；

proof

充分性：

若$x$是$C$ 的极点，采用反证法，若$C$包含直线，则存在这样的集合 ${\bar{x} +\alpha d|\alpha \in R, d \ge 0 }$ 则 $d$ 和$-d$ 都是过$\bar{x}$ 点的回收方向， 由回收锥定理，一个集合中的一点处的回收方向也是集合中其余任一点的回收方向，即在$x$ 也存在 $x + \alpha d \in C, x - \alpha d \in C$ 这与$x$ 是极点矛盾，顾假设不成立，$C$不能包含直线；

必要性：

采用数学归纳法证明必要性：

$C \subset \mathbb{R^n}$ ,

当$n=1$时， 一个点的集合，极点即他自身

当$n=k$ 时， $C$ 是$k$ 维空间的子集，此时结论成立，

当$n= k+1$时， 构造这样一个点：

$x \in C, y \notin C$ , $\bar{x}$ 是连接$x, y$ 的直线与$C$的交点，则$\bar{x}$ 不是$C$的内部， 由支撑超平面定理, $\bar{x}$处存在支撑超平面；

即 $\exists\ a \neq 0$ 使得 $a^Tx \le a^T\bar{x} , \forall x \in C$ ，这是一个超平面$H$;

因为$C \cap H \subset \mathbb{R^k}$ , 而在$n=k$ 时结论是成立的，也就是$C \cap H$ 存在极点 ，依据命题1 ，$C$ 也存在极点。证毕；

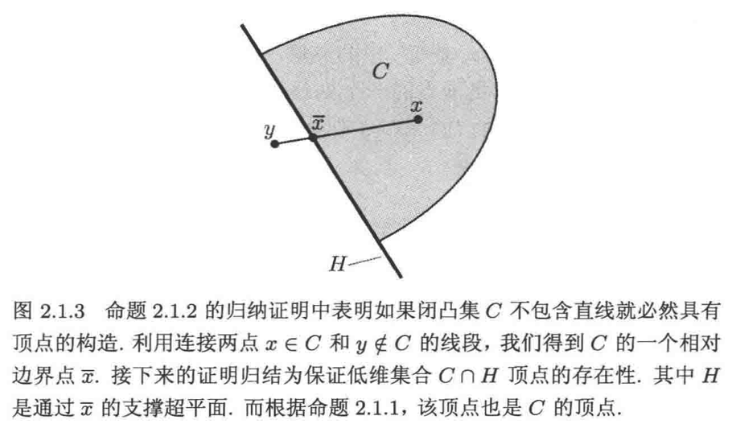
命题3

$C$ 是一个非空闭凸子集，假定对某个秩为$n$ 的矩阵 $A$ 和某个$b$ 存在

$$Ax \ge b, \ \forall x \in C$$

则$C$ 至少存在一个顶点；

命题4 多面体集的顶点存在条件

对于多面体集合：

$$P = \{x |\ a_j^Tx \le b_j ,\ j=1,2,...,r \}$$

$v \in P$ 是顶点 $\iff$ $A_v = \{a_j | a_j^Tv=b_j \}$ 包含$n$ 个线性无关的向量；

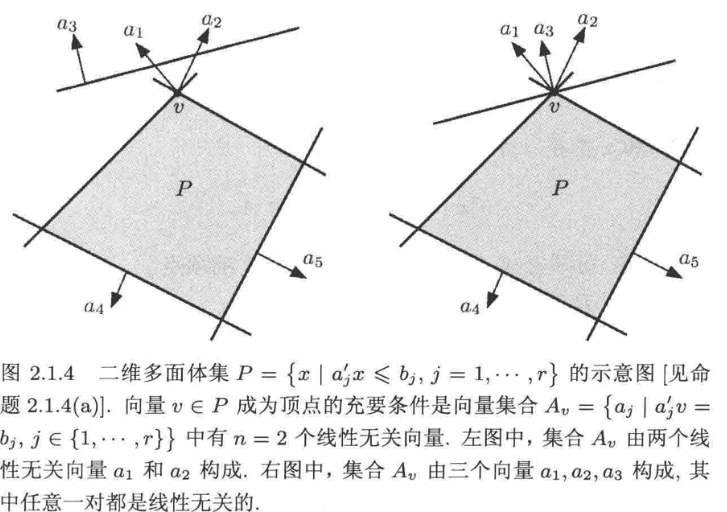
命题5

多面体集

$$\{x | a^T_jx \le b_j, j=1,2,3...,r \}$$

存在顶点 $\iff$

集合

$$\{a_j |j=1,2,3...r \}$$

包含$n$ 个线性无关向量；

极锥 (Polar Cone)

$C$ 的极锥记做$C^*$ 定义为：

$$C^* = \{y | y^Tx \le 0,\ \forall x \in C \}$$

$C^*$是锥体，而且是一组闭半空间的交集，他是闭的且凸的，（不管$C$ 是否是凸的）；

命题6 极锥定理

对于任意非空集合$C$:

$$(a)\ C^* = (cl(C))^* = (conv(C))^* = (cone(C))^*$$

对任意非空锥体$C$, 有

$$(C^*)^* = cl(conv(C))$$

特别的，如果$C$是闭凸集，有$(C^\star)^\star = C$

Proof

(1) 证明 $C^{\star}= (cl(C))^{\star}$， 证明两集合相等需要证明互为彼此子集；

a. $\forall X, Y$ 若 $X \subseteq Y$ , 则有 $Y^{\star} \subseteq X^{\star}$ ; 因为$C \subseteq cl(C)$ 则有 $(cl(C))^{\star} \subseteq C^{\star}$

b. 若$y \in C^{\star}$, 对于 序列${x_k} \subset C$ 都有 $y^Tx^k\le0$ ; 因为序列的极限就是集合的闭包，则对于$x \in cl(C)$ 也有$y^Tx\le 0$, 所以 $y \in cl(C)^{\star}$ ; 则$C^{\star} \subseteq cl(C)^{\star}$

所以两者互为子集，两个集合相等；

(2) 证明 $C^{\star} = (conv(C))^{\star}$

a. 同样的根据$C \subseteq conv(C)$ 得出 $(conv(C))^{\star} \subseteq C^{\star}$

b. 若$y \in C^{\star}$ , 对于任意$x \in C$ 则有 $y^Tx \le 0$ , 那么对于所有$x$的凸组合的$z$ ,也一定有$y^Tz \le 0$

因此有$y \in conv(C)^{\star}$ ; 即 $C^{\star} \subseteq (conv(C))^{\star}$

(3) 证明 $C^{\star} = (cone(C))^{\star}$ 差不多的证明思路；

多面体集和多面体函数

多面体锥和有限生成锥

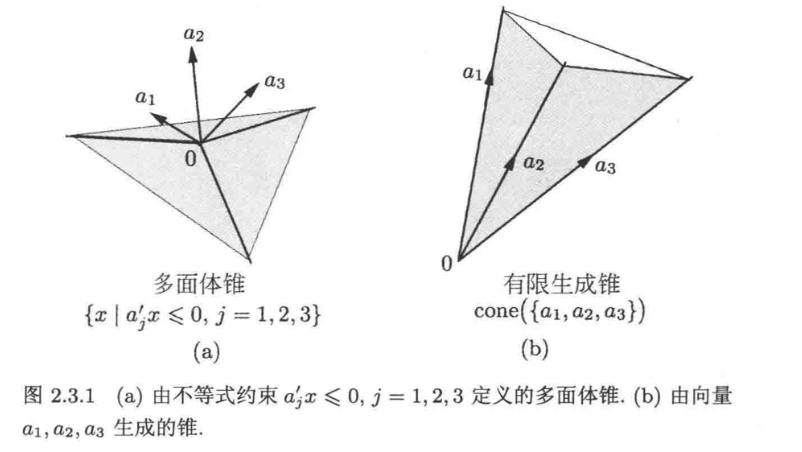
多面体锥相比较 多面体集的特点是 他要经过原点；

Farkas引理

令 $a_1,a_2, … ,a_r $都是空间中的向量，则多面体锥 ${x |a^T_j x \le 0 }$ 和有限生成锥 $cone({a_1, …a_j})$ 都是闭的，且互为极锥

他有另外一个常用的版本，又叫择一性定理：

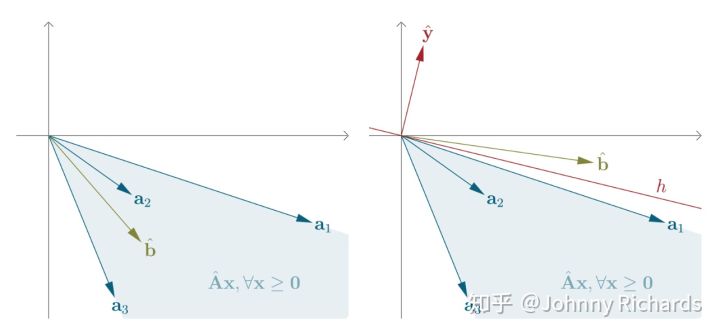
$A$是$m \times n$ 矩阵， 则下面两组方程只有一组有解：

$$Ax = b,x\ge 0, x\in R^n \ (1) \\ A^Ty \le 0, b^Ty \gt 0, y\in R^m \ (2)$$

从几何意义上解释， (1) 是说b 落在$A$ 张成的锥中， (2) 是说$b$ 在锥外；

那么这个引理也就是说对于向量$b$ ，只可能存在两种互斥情况：（1） $b$在这个凸锥里。（2）$b$在这个凸锥外。[1]

Minkowski-Weyl 表示定理

集合$P$是多面体 $\iff$ 存在非空有限集${v_1, v_2, …,v_m}$ 和有限生成锥 $C$ 使得 $P = conv({v_1,…,v_m}) + C$

即

$$P = \{x\ |\ x = \sum_{j=1}^m \mu_jv_j + y,\ \sum_{j=1}^m\mu_j=1,\ \mu_j \ge 0,\ j=1,2,...,m,\ y \in C \}$$

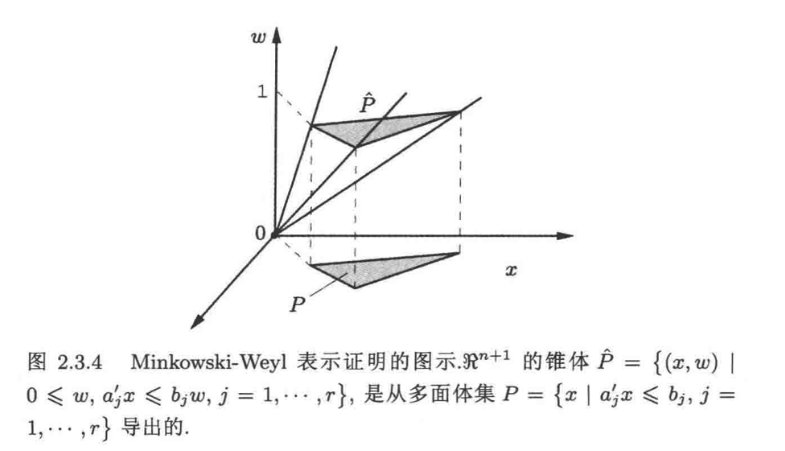
多面体的代数运算

• 多面体集的交如果非空，则为多面体
• 多面体集的笛卡尔积是多面体
• 多面体在线性变化下的像是多面体
• 两个多面体集合的向量和是多面体’
• 多面体集在线性变换下的原像是多面体

Reference

• [1] 知乎-如何理解Farkas引理
• 《Convex Optimization Theory》
• 老师的课件