[stat 06] 多元统计分析

March 16, 2020, Zhengzhou

多元统计分析

均值向量的检验

单样本均值向量$\mu$的检验 （$\Sigma$ 已知）

待检验问题： $H_0: \bold{\mu} = \mu_0 \ vs . \ H_1: \mu \neq \mu_0$ 检验统计量： $Z^{2}=n\left(\overline{\mathbf{y}}-\boldsymbol{\mu}_{0}\right)^{\prime} \boldsymbol{\Sigma}^{-1}\left(\overline{\mathbf{y}}-\boldsymbol{\mu}_{0}\right)$ 统计量原假设分布： $Z^2 \sim^{H_0} \chi^2(p)$ 拒绝域： $Z^2 > \chi_{\alpha}^2(p) \\ P(Z^2 >c|H_0) = \alpha$ 构造均值向量与估计的马氏距离为检验统计量，这个统计量服从卡方分布。

两个一元检验都不能拒绝$H_0$, 但是由于$Y1,Y2$ 之间有相关关系，多元检验可以拒绝$H_0$

单样本均值向量检验 （$\Sigma$未知）

检验统计量： $Hotellings: T^{2}=n\left(\overline{\mathbf{y}}-\boldsymbol{\mu}_{0}\right)^{\prime} \boldsymbol{S}^{-1}\left(\overline{\mathbf{y}}-\boldsymbol{\mu}_{0}\right)$ 原假设分布： $T^2 \sim T^2(p, n-1)$

两样本均值向量检验：独立样本

前提假设：$p$ 维样本 $y_{11}, y_{21}, ..., y_{1n_{1}} \sim N_p(\mu_1, \Sigma) \\y_{21}, y_{22}, ..., y_{2n_{2}} \sim N_p(\mu_2, \Sigma)$ $\Sigma$是未知的共同协方差矩阵。

检验问题 $H_{0}: \boldsymbol{\mu}_{1}=\boldsymbol{\mu}_{2}, \text { vs. } H_{1}: \boldsymbol{\mu}_{1} \neq \boldsymbol{\mu}_{2}$ 检验统计量： $T^{2}\left(=\frac{\left.n_{1} n_{2}\right)}{n_{1}+n_{2}}\left(\overline{\mathbf{y}}_{1}-\overline{\mathbf{y}}_{2}\right)^{\prime} \mathbf{S}_{p l}^{-1}\left(\overline{\mathbf{y}}_{1}-\overline{\mathbf{y}}_{2}\right)\right. \\ \mathbf{S}_{p l}=\frac{\left(n_{1}-1\right) \mathbf{S}_{1}+\left(n_{2}-1\right) \mathbf{S}_{2}}{n_{1}+n_{2}-2}$ 仍然服从Hotelling 分布： $T^{2} \stackrel{\mathrm{H}_{0}}{\sim} T^{2}\left(p, n_{1}+n_{2}-2\right)$ 拒绝域： $T^{2}>T_{\alpha}^{2}\left(p, n_{1}+n_{2}-2\right)$

两样本均指向量检验（成对出现）

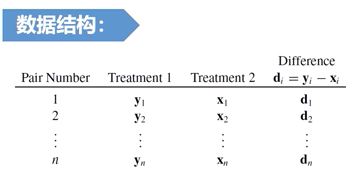
待检验问题： $H_{0}: \delta=\mathbf{0}, \text { vs. } H_{1}: \delta \neq 0$ 检验统计量及其假设分布： $T^{2}=n \overline{\mathbf{d}}^{\prime} \mathbf{S}_{d}^{-1} \overline{\mathbf{d}} \stackrel{H_{0}}{\sim} T^{2}(p, n-1)$

主成分分析

总体PCA

记原始变量$y = (Y_1, …, Y_p)^T$ ， 其协方差矩阵$\Sigma$, 主成分分析试图定义一组互不相关的变量，称为$Y$的主成分，记为$Z_1, …, Z_p$, 每一个主成分都是$Y_1,…,Y_p$的线性组合 $Z_i = a_i^Ty$

则$Var(Z_j) = a_j^T\Sigma a_j$, $Cov(Z_j, Z_k) = a_j^T\Sigma a_k$

目标函数：方差反应信息量大小，我们期望$Z_1,…Z_p$ 按方差大小排序，同时满足互不相关（协方差为0） $Z_1= a_1^Ty\\ a_1^Ta_1=1 \\$

因子分析

对于$p$ 个原始变量$Y_1,…,Y_p$ 来说，那些高度相关的变量很可能会遵循一个公共的潜在结构–或可称之为公共因子 Common Factor. 因子分析旨在提出因子模型来研究如何用几个公共因子，记做$F_1, …,F_m$ ， 通常$m <p$, 来刻画原始变量之间的相关性。 $Y_1 = l_1F + \epsilon_1 \\ Y_2 = l_2F + \epsilon_2 \\ Y_3 = l_3F + \epsilon_3$ $F$ 公共因子；$\epsilon_j$ 特殊因子； $l_j$ 系数，载荷； $\mathbf{y}-\boldsymbol{\mu}=\mathbf{L} \mathbf{f}+\boldsymbol{\varepsilon} \\ Cov(\mathbf{y}, \mathbf{f}) = \mathbf{L}$