[cvp06] Duality Theory

时间： 2019-12-19 创新岗 第六周课

这周是倒数第二次凸分析课程，进入到了凸优化最关键的思想–对偶。同《凸优化与最优化方法》不同，凸分析课程主要从集合的角度探究对偶理论。这次的主要内容有：

• 部分极小化、极大极小问题
• MC/MC 几何对偶框架

如果你在凸优化方法课程中找不到很自然的对偶原理的得出，那么凸分析就是探究本源的课程。对偶性的本质在于闭的凸集有两种等价的描述方式：用该集合的所有点的并集来描述，或用与其共轭函数相关的一组超平面的闭半空间交集描述；

部分极小化

Theorem 函数$F : \mathbb{R^{n+m}} \rightarrow (-\infty, \infty]$ , 设函数$f: \mathbb{R^n} \rightarrow [-\infty, \infty]$ 定义如下： $f(\boldsymbol{x})=\inf _{\boldsymbol{z} \in \mathbb{R}^{m}} F(\boldsymbol{x}, \boldsymbol{z})$ 则有以下结论：

• 若$F$ 是凸函数，则$f$ 是凸函数；

• 记算子$P$ 是对$(x, w)$空间的投影， 即对于$\mathbb{R^{m+n+1}}$ 的任意子集$S$ 有

$$P(S) = {(x, w)

\ (x,w,w) \in S }$$,则有

• $$P(epi(F)) \subseteq epi(f) \subseteq cl(P(epi(F)))$$

这个定理是从函数上图讨论了部分极小化函数的凸性和闭性，下图的例子很直观：

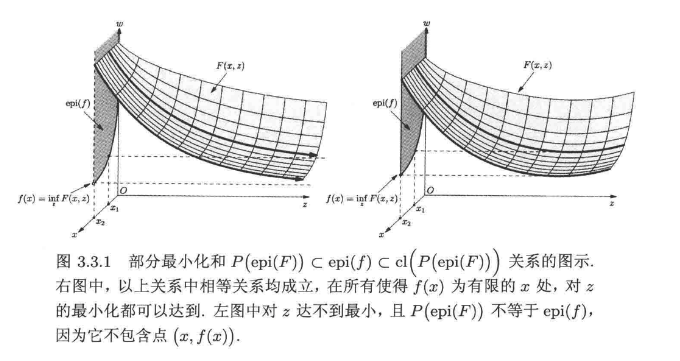
这里我们再来回顾一下凸函数的连续性：

• 实数域的凸函数一定是连续函数；如果是正常函数，则在定义域的相对内部连续；
• 上图是闭集（函数是闭的）、函数上半连续、函数水平集是紧集；三者互相等价；

极大极小问题

设 $\phi : X \times Z \rightarrow R$是闭凸函数，想其中$X,Z$ 分别是$\mathbb{R^n}, \mathbb{R^m}$ 的非空子集，极大极小问题研究的主要是：

$$\sup _{\boldsymbol{z} \in Z} \inf _{\boldsymbol{x} \in X} \phi(\boldsymbol{x}, \boldsymbol{z})=\inf _{\boldsymbol{x} \in X} \sup _{\boldsymbol{z} \in Z} \phi(\boldsymbol{x}, \boldsymbol{z})$$

什么时候相等，且各自的极值都能取到；

各自取到最优且相等的解称为鞍点(saddle point)， 即满足：

$$\sup _{z \in Z} \phi\left(\boldsymbol{x}^{*}, \boldsymbol{z}\right)=\phi\left(\boldsymbol{x}^{*}, \boldsymbol{z}^{*}\right)=\inf _{\boldsymbol{x} \in X} \phi\left(\boldsymbol{x}, \boldsymbol{z}^{*}\right)$$

这个问题让我们联想到了在凸优化经典的约束优化转换的形式：

$$\min _{\boldsymbol{x}} f(\boldsymbol{x}) \quad \text { s.t. } \boldsymbol{x} \in X, \boldsymbol{g}(\boldsymbol{x}) \leq \mathbf{0}$$

写出拉格朗日函数：

$$L(\boldsymbol{x}, \boldsymbol{\mu})=f(\boldsymbol{x})+\sum_{j=1}^{r} \mu_{j} g_{j}(\boldsymbol{x})$$

原问题等价于现在的无约束形式：

$$\min _{\boldsymbol{x}} \sup _{\boldsymbol{\mu} \geq 0} L(\boldsymbol{x}, \boldsymbol{\mu}) \quad \text { s.t. } \boldsymbol{x} \in X$$

那么他的对偶形式为：

$$\max _{\boldsymbol{\mu}} \inf _{\boldsymbol{x} \in X} L(\boldsymbol{x}, \boldsymbol{\mu}) \quad \text { s.t. } \boldsymbol{\mu} \geq \mathbf{0}$$

对偶问题都是凸问题，现在研究目标转为两个问题的最优目标什么时候相等；

凸优化方法课程下一步会讨论强弱slater条件 使得对偶间隙为0；然后分析出最优性解满足的KKT条件；

而凸分析不直接研究，我们首先从几何上的一个框架来描述原问题与对偶问题，来说明为什么存在对偶间隙，以及弱对偶定理为什么成立，进一步看出什么时候强对偶成立；而最优解的条件需要在下一讲借助其他工具描述；

MCMC对偶框架

MCMC这个缩写有另一个更广为人知的方法：蒙特卡洛马尔科夫采样模型。

而在凸分析理论中，他指的是两类几何问题；

• 极小公共问题 (Minimal Common Problem)

$$\begin{array}{l}{\text { minimize } w} \\ {\text { subject to }(0, w) \in M .}\end{array}$$

他的最优解为

$$w^{*}=\inf _{(0, w) \in M} w$$

• 极大交叉问题(Maximal Crossing Problem)

文字描述就是能将集合包含进他的闭半空间的超平面与$(n+1)$ 轴交点的最大值；

超平面可以描述为：

$$H_{\mu, \xi}=\left\{(u, w) | w+\mu^{\prime} u=\xi\right\}$$

集合被包含需满足的条件为：

$$\xi \leqslant w+\mu^{\prime} u, \quad \forall(u, w) \in M$$

即

$$\xi \leqslant \inf _{(u, w) \in M}\left\{w+\mu^{\prime} u\right\}$$ $$q(\mu)=\inf _{(u, w) \in M}\left\{w+\mu^{\prime} u\right\}$$

则 最大交点问题转化为求函数$q(u)$ 的最大值及对应的$\mu$ 值：

$$\begin{array}{l}{\text { maximize } q(\mu)} \\ {\text { subject to } \mu \in \Re^{n} .}\end{array}$$

对偶问题的最优值为：

$$q^{*}=\sup _{\mu \in \Re^{n}} q(\mu)$$

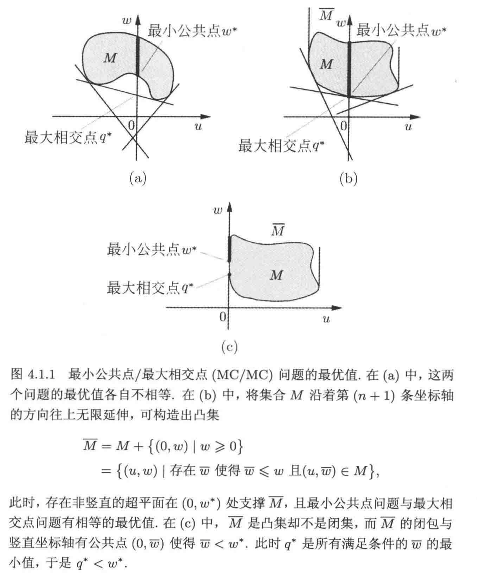
凸优化的核心理论都会统一到在这两个基本问题组成的集合框架下；

几个定理：

Theorem 对偶函数$q$ 是上半连续的凹函数

Theorem(弱对偶定理) 不等式 $q^\star \le w^\star$ 恒成立；

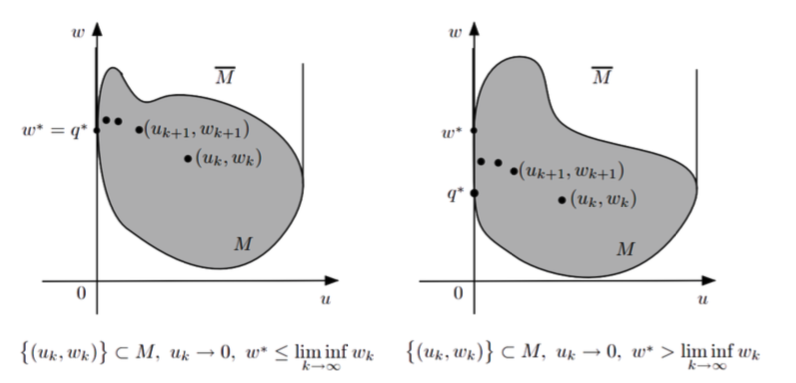
**Theorem(强对偶定理) ** 在MCMC框架下：

• 集合$$\bar{M} = M + {(0, w)

  w\ge 0 }$$ 为凸集

• $w^\star \lt \infty$
• 强对偶成立 $q^\star = w^\star$

$\iff$ 对于任意序列${(\mu_k, w_k) } \subseteq M$, 当$\mu_k \rightarrow 0$时有 $w^\star \le \lim \inf_{k\rightarrow \infty} w_k$

下图是直观的几何解释：

例：约束优化对偶性

现在让我们忘掉拉格朗日函数、拉格朗日对偶函数、拉格朗日乘子，总之就是忘掉拉格朗日。单纯从上述的两个几何问题框架得出一般约束优化问题的对偶形式。

$$\begin{array}{c}{\min _{\boldsymbol{x}} f(\boldsymbol{x})} \\ {\text { s.t. } \boldsymbol{x} \in X, \boldsymbol{g}(\boldsymbol{x}) \leq \mathbf{0}}\end{array}$$

我们针对极小公共问题构造一个函数：

$$F(\boldsymbol{x}, \boldsymbol{u})=\left\{\begin{array}{ll}{f(\boldsymbol{x})} & {\boldsymbol{x} \in C_{\boldsymbol{u}}} \\ {\infty} & {\boldsymbol{x} \notin C_{\boldsymbol{u}}}\end{array}\right. \\ C_{\boldsymbol{u}}=\{\boldsymbol{x} \in X | \boldsymbol{g}(\boldsymbol{x}) \leq \boldsymbol{u}\}, \boldsymbol{u} \in \mathbb{R}^{r}$$

这个函数就是把原来 的与$(0,w)$轴的交点变得一般化。同时赋予$u$ 的含义是约束；

而针对约束优化问题，原问题的表达：

$$\begin{aligned} p(\boldsymbol{u}) &=\inf _{\boldsymbol{x} \in \mathbb{R}^{n}} F(\boldsymbol{x}, \boldsymbol{u}) \\ &=\inf _{\boldsymbol{x} \in X, \boldsymbol{g}(\boldsymbol{x}) \leq \boldsymbol{u}} f(\boldsymbol{x}) \end{aligned}$$

最优解：

$$w^{*}=p(\mathbf{0})=\inf _{\boldsymbol{x} \in X, \boldsymbol{g}(\boldsymbol{x}) \leq 0} f(\boldsymbol{x})$$

那么现在是$w$ 和$u$ 都赋予了定义，我们只需根据极大交叉问题的形式仿照写出对偶问题：

$$\begin{aligned} q(\boldsymbol{\mu}) &=\inf _{u \in \mathbb{R}^{r}}\left\{p(\boldsymbol{u})+\boldsymbol{\mu}^{\top} \boldsymbol{u}\right\} \\ &=\inf _{x \in X, g(x) \leq u}\left\{f(x)+\boldsymbol{\mu}^{\top} \boldsymbol{u}\right\} \\ &=\left\{\begin{array}{ll}{\inf _{x \in X}\left\{f(\boldsymbol{x})+\boldsymbol{\mu}^{\top} \boldsymbol{g}(\boldsymbol{x})\right\}} & {\boldsymbol{\mu} \geq 0} \\ {-\infty} & {\text { otherwise }}\end{array}\right.\end{aligned}$$

这一步是非常自然的，他跟使用拉格朗日理论得出的对偶形式是一样的。而拉格朗日理论使用其他方法证明了对偶性质，强弱对偶性等，而我们用MCMC得出的形式天然具有对偶性质；

例2 线性规划对偶

我们再比葫芦画瓢写一下线性规划的对偶：

$$\begin{array}{cl}{\min _{\boldsymbol{x}}} & {\boldsymbol{c}^{\top} \boldsymbol{x}} \\ {\text { s.t. }} & {\boldsymbol{a}_{j}^{\top} \boldsymbol{x} \geq b_{j}, j=1, \ldots, r}\end{array}$$

原问题

$$p(u) = \inf _{b-Ax \le u} f(x)$$

原问题最优解：

$$w^\star = p(0)$$

对偶问题：

$$q(u) = \inf_u \{\mu^Tu +p(u) \} \\= \inf_{b-Ax \le u} \{\mu^Tu + c^Tx \} \\ = \inf_x \{\mu^T(b-Ax) + c^Tx \},\ \mu \ge 0 \\ = \mu^Tb ,\ c^T- A\mu=0$$

总结：上述两个例子并非要论证MCMC框架的对偶描述要优于lagrange, 而是验证MCMC理论的本源性，与lagrange得出的结论一致也间接说明了lagrange那套相对简单思维的推导是有基础理论支持证明的。

好了，到目前这只是MCMC框架理论的冰山一角，所有的凸优化理论都可以使用MCMC对偶框架来解释。下一讲将接着探索最优解的性质。这也是凸优化问题解答的关键。

Reference

• 老师的课件